On the Topology of State-space, Linear vs. Nonlinear Theories and Dry Friction

 

Insights in Mining Science & Technology Juniper Publishers

Authored by  Jozsef Verhas

Abstract

The work reported here aimed to eliminate the gap between static- and sliding friction on the ground of non-equilibrium thermodynamics with dynamic (internal) degrees of freedom introduced into the state space of the system. Here a germ of a thermodynamic theory is sketched without acquiring generality. Here the simplest model is looked for to eliminate the gap between static and kinetic friction. It is not a complete idea at all but may be a guideline for further modeling. The fork where the train of thoughts stops at gives way to several kinds of possibilities, a number of which by the author’s opinion may have their own realm of application. Finally, an accurately accountable model is given that may be assumed friction if we pretend not knowing its origin and the law differs signficantly from the nearly exclusively used Coulomb’s law.

This example supports the idea that friction cannot be described in a simple and uniform theory.

Keywords: Non-equilibrium system; Topological space; Thermodynamics; Chemical reactions; Fluid turbulence; Dry friction; Onsagerian sense; Rheology

Introduction

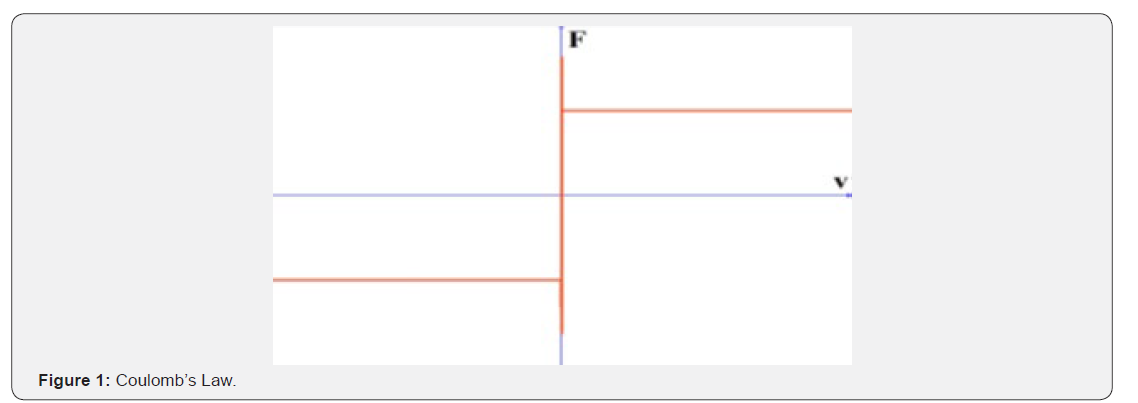
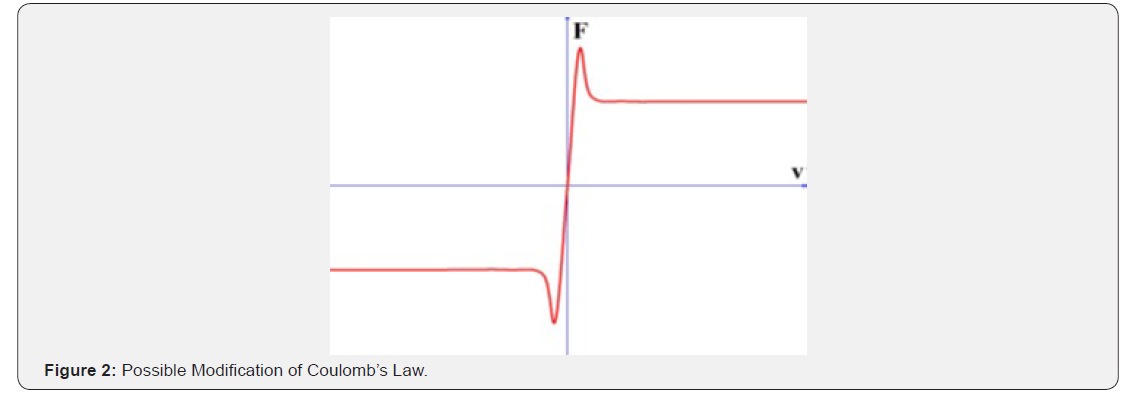
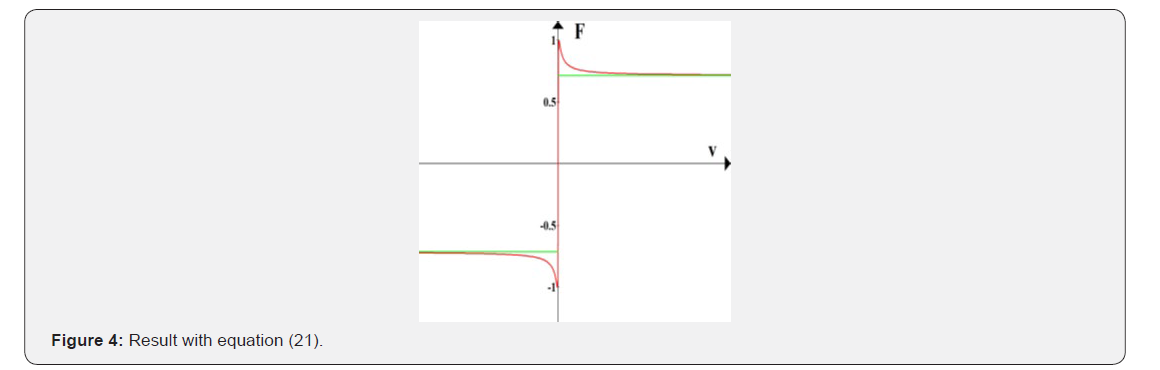
The possible states of a non-equilibrium system can be assumed a topological space. Let a neighbourhood of a point (a state) be the set of those points that cannot be distinguished with the help of an observation (measurement). The intersection of two environments of a point x is obviously the set of those that are distinguished none of the two observations. Similarly, the elements of their union are the set of points not distinguished by at least one of the observations. The environments of the points together with their union and finite intersections define the open sets. The topology defined this way is very important but too general for practical purposes, so we are looking for more familiar ones. Classical thermodynamics has been satisfied with the topology of a finite linear space in any case and non-equilibrium thermodynamics most often remained in the vicinity; the fields of the variables used by the equilibrium theory have been introduced in classical irreversible thermodynamics, and similarly, fields of a finite number of coordinates are used in extended thermodynamics and the theories with dynamic (internal) variables. Rational thermodynamics goes further. The finite linear space is replaced by function space. Another question concerns linearity. The linear approximations are easier to deal with and, in many cases, result in usable outcome; but there are problems a linear theory cannot deal with. Such problems are those of chemical reactions, fluid turbulence, and dry friction the present paper fo cuses on. Nevertheless, sliding friction is frequent and it was the first irreversible process we were faced in the school, a very rare e ort has been aimed to develop its non-equilibrium thermodynamic theory. The reason may be guessed as Coulomb’s (Amontons’ 3rd) law is often taught as if it where the final solution, even the velocity dependence of the friction force is rarely mentioned in textbooks or in papers, looking away from its direction. On the other hand, the phenomenon cannot be accounted with a linear theory even in the Onsagerian sense. Coulomb’s law displays a strong singularity at equilibrium, which is, at least, extremely rare in nature. On the ground of the thermodynamic theory of rheology, one can guess, that the singularity is virtual. The friction force does depend on the magnitude of the velocity and the function is continuous, but it starts so steeply and falls back at practically very low values that to observe it is difficult. If the two solids are separated with a thin layer of a non-Newtonian fluid the thermodynamic theory of the latter can be applied. This is not a nonsense; the independence of the friction force on the contact area is explained by rather widely accepted ideas with the plastic flow of the materials at the surface region. In the last decades, the interest has increased, and several theories were published and experimentally verified that explain friction and wear at different circumstances and the results are not like to each other nor to Coulomb’s law. Applying Onsager’s thermodynamics beyond the realm of linearity is like guessing. Not a free brainstorm, but severely limited by observations. Here a germ of a thermodynamic theory is presented always keeping an eye on the topology of the state space. Nevertheless, sliding friction is frequent [1, 2] and it was the first irreversible process we were faced in the school and probable one of the most important from technological point of view, very rare effort [3] has been aimed to develop its non-equilibrium thermodynamic theory if ever, even though, non-equilibrium thermodynamics [4- 18] has been applied to several phenomena with full success [18- 29]. The reason may be guessed as Coulomb’s law is often taught as if it where the final solution, even the velocity dependence of the magnitude of friction force is rarely mentioned in textbooks or in papers. On the other hand, the phenomenon cannot be accounted with a linear theory even in the Onsagerian sense. Coulomb’s law is highly non-linear and displays a strong singularity at equilibrium as shown in Figure 1 which is, at least, extremely rare in nature. Starting from the fact that the static friction is larger than the kinetic one, we may assume that the friction force at very slow-motion increases with decreasing velocity. At the end of the 19th century the low velocity meant rom 3mm/s down to 0.06mm/s [30] while nowadays from 1000nm/s down to 1nm/s, approximately 7 molecules per second. The experiments support the suspicion. Amontons’ 3rd law may be replaced with a function free of the strong singularity just at equilibrium. On the ground of the thermodynamic theory of rheology, [18], one can guess, that the singularity is virtual. The friction force does depend on the magnitude of the velocity and the function is continuous, as shown in Figure 2, but it starts so steeply and falls back at practically very low velocities that it is difficult to observe.

Thermodynamic Theory

The assumed system is two rigid bodies in contact and sliding on each other. Motion is assumed tangential to the surface. The first law of thermodynamics reads

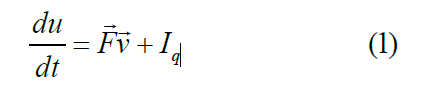
where u is the internal energy, F → is the applied force necessary for steady slip with velocity v→ , I_q the heat flow, and t is the time. The second law reads

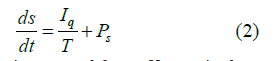
in general form. Here s is the entropy, T the temperature both system and the environment, and s P is the entropy production in unite time.

Model in local equilibrium

If local equilibrium is supposed than the entropy of the system depends on the internal energy alone;

which results

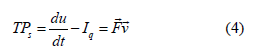
and for the linear Onsager law

The linear approximation is obviously not able to fulfill the needs. In nonlinear approximation L may depend on the velocity rather arbitrarily; the only requirement of the second law is

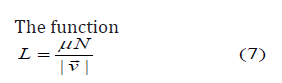
gives back Coulomb’s law for sliding but knows nothing on static friction, moreover, L has severe singularity at equilibrium. The symbol μ stands for the coefficient of sliding friction and N for the normal force pressing the surfaces one to the other. If a function the graph of which is something like the line in Figure 2 is taken, then a better formula is obtained. The disadvantages are that such a function is not very simple at all and the function must be measured or guessed. I incline to abandon the hypothesis of local equilibrium2.

Model with one dynamic variable.

The first approximation out of local equilibrium is based on a single dynamic variable α → invariant under time inversion. It is assumed to be a vector because the local equilibrium theory contains vectorial force and flux. Basing on the Morse lemma, [31], the entropy is given as

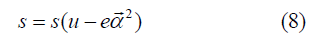
leading to

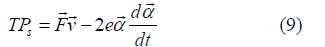
where e is a convenient positive constant not specified yet.

The linear laws take the form

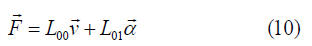
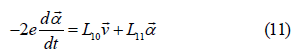
Here, the sliding surfaces are supposed isotropic. The thermodynamic forces are taken v→ and α → . The Onsager-Casimir reciprocal relation [4, 32] reads

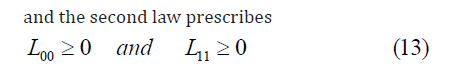
and nothing else. The linear theory is again unsatisfactory as displays a force proportional with the velocity for motion; non-linear material laws are indispensable. The term 00 L v→ is increasing without limit if L₀₀ remain finite except it is zero or tends to zero. For low velocities α→ is approximately proportional to the velocity, so for the starting section of the force, an L₀₁ depending properly on α → is needed. Such a function can be found with the analogy to non-Newtonian fluids, especially, to Maxwell’s fluid, in rather simple form, say

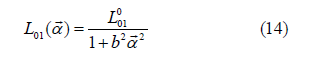
which involves also

if L₁₀ is assumed constant. The analogy to the Maxwell- fluid is motivated by the idea that the parameter

→ is something like an overall account on the rotation, as well as, the deformation of the bounds between the surfaces sliding on each other, whatever their physical nature is. A simpler choice for L₀₁(α →) is

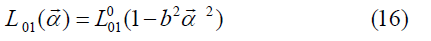
which is a polynomial approximation of L₀₁ (α →) . Further on, this choice will be used. The proportionality of α → to the velocity in stationary motion has to be dropped for high velocities, because it leads to increasing force, contrary to Coulomb’s law. The simplest choice is L₀₀ = 0 . With this choice, 10 L cannot be constant any longer, the second law requires the validity of equation (12) in complete generality. This case the force tends to zero with increasing. To get rid of the discrepancy, 11 L is replaced by a function having a pole limiting the magnitude of α → . The simplest function

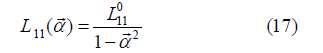
may lead to the needed rule for the force. Such a pole may be the consequence of the limited amount of non-dissipated energy. (The quantity e is chosen to that.) The constitutive equations read

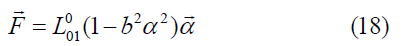
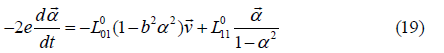
The coefficient b can be determined from the static and dynamic coefficients of friction:

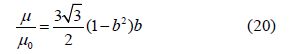
To get a function (F→ v→) for stationary sleep similar to one in Figure 2 the parameter b has to be bigger than 1 3 and if b ≥1the friction tends to zero for high velocities. The presented model is only one from many many other possibilities. A very similar graph is resulted by the function

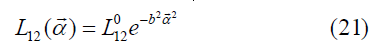
which seems quite natural if friction is due to chemical bounds. A non-linear law similar to the above is giving account on the static friction also with creep and that the friction force is independent of the velocity if it is high enough. For some materials, decreasing force has been reported at very low velocities [33].

Further considerations

The model presented here gives account on continuous and delayed change of the friction force when the velocity changes abruptly, but the account is not good. This model does not display the overshot found experimentally. This fact makes plausible that the coefficient 11( ) L α → cannot be zero but at α = 1. It may be something like

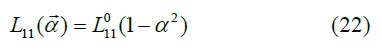
and 12(L α →) |together with 21(L α →) of course may be stretched with a constant term; perhaps with a negative one. The unlimited validity of the Onsager-Casimir reciprocal relation eq. (12) ensures positive entropy production; it is a enough but necessary condition. This sketch has to be examined in the future.

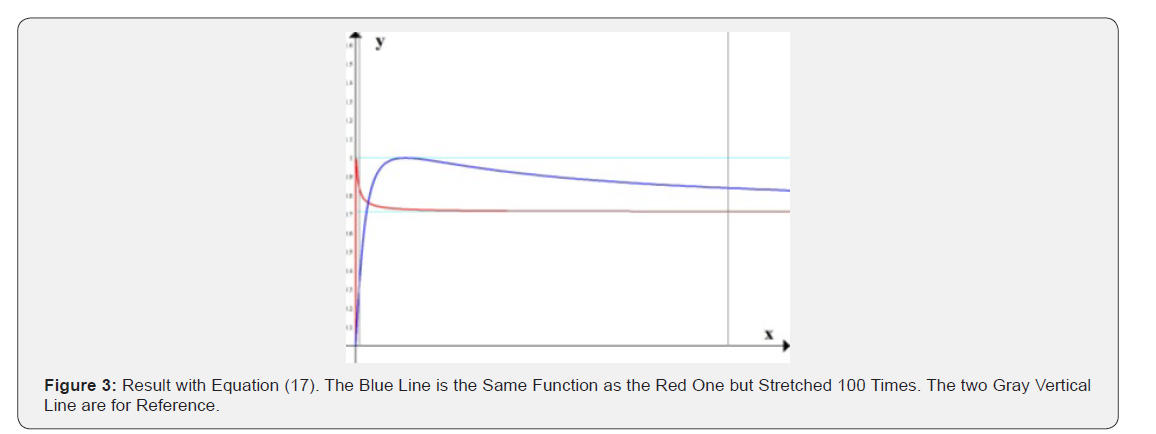
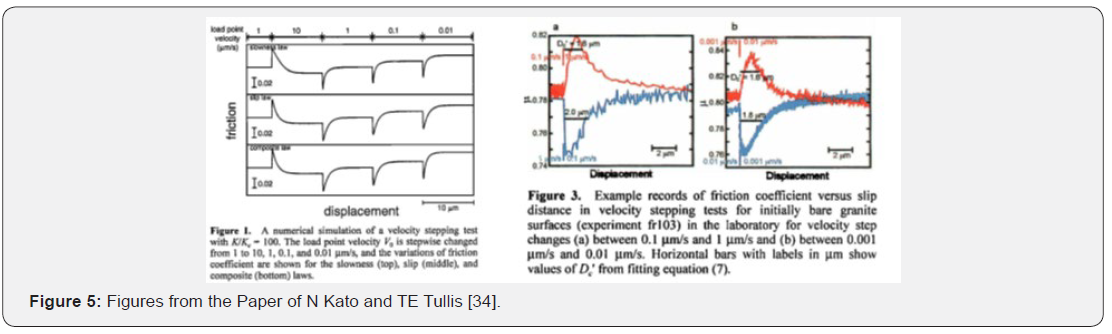
But there is some other possibility, as well. The graphs in Figure 3. In the paper [34] awakens the suspicion that two relaxations occur, i.e. two dynamic degree of freedom is needed Figure 4 & 5.

Model with two dynamic variables

With two dynamic degrees of freedom, the entropy function reads

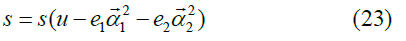
and the dissipation function is

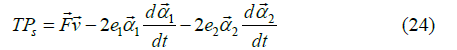
The (non-linear) Onsager-equations may be written in general form as

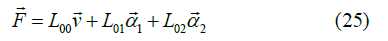
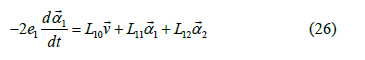
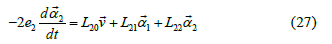
Keep in mind, that the Like coefficients do depend on te thermodynamic forces 1 2 (v→,α→ ,α→ ) and they are not uniquely de fined. Moreover, similar can be said on the dynamic variables. In the linear theory, the set of equations concerning the relaxation of the dynamic variables (if v = 0) may be transformed to diagonal form if Onsage’s reciprocal relations hold, and this is valid in the non-linear theory, too. (See in appendix). Motivated by this,

is taken, moreover, L₀₀ = 0 and L₂₁ = −L₂₁ = 0 are assumed. keeping the consideration on the limited amount of undissipated energy belonging to 1 α → leads to the assumption, that both L₁₁ and L₂₂ have pole at 1 α =1. (L₁₁ and L₂₂ must depend similarly on the dynamic variable. See Lemma 2 in the appendix.) With this presumption the equations turn to

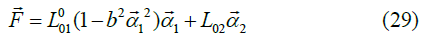
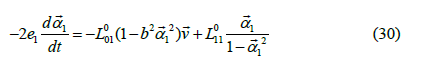
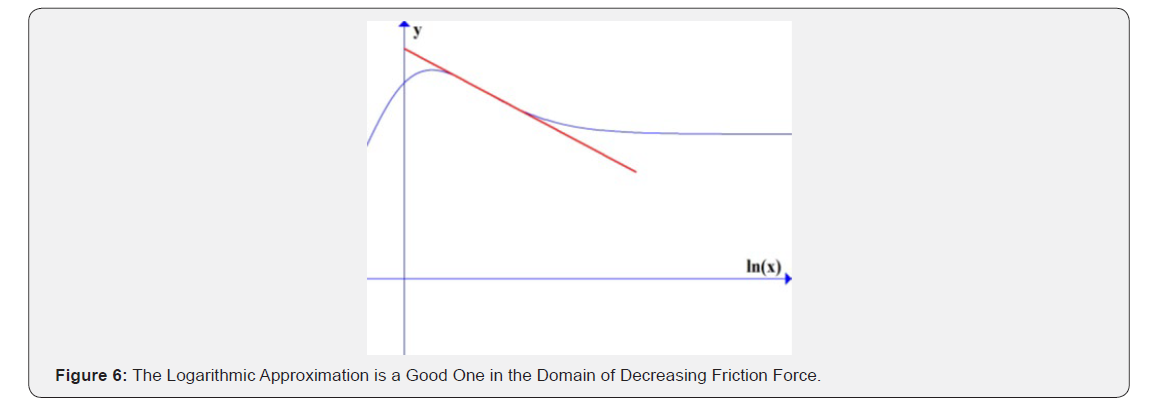
The content of them says that the two-dynamic degree of freedom contribute to the force independently from each other. For a stationary sleep the force, the velocity, and even 2 α can be given in parametric form with α₁ . The plot with representative parameters in Figure 6 shows that the logarithmic approximation fits well in the domain where the friction decreases with sleep velocity. And as for the overshot, the contribution of 1 α to the force is decreasing for large enough α₁ but that of 2 α is monotone increasing; so, if the relaxation of α₂ is faster than that of α₁ the overshot reported in the example records in the paper of Kato and Tullis [KT01] (in Figure 3.) has been explained, too.

Conclusions

Here the skeleton of a thermodynamic theory has been sketched without acquiring generality. It is not a complete idea at all but may be a guideline for further development. The fork where the train of thoughts stops at gives way to several kinds of possibilities, a number of which by the author’s opinion may have their own realm of application. I incline to believe that friction is a great family of processes and each kind needs its own theory, but the one presented here may be a good common approximation for each case. If the two solids are separated with a thin layer of a non-Newtonian fluid or if the contact area is surrounded by a thin fluidal layer (self-lubrication) then the thermodynamic theory of the former can be applied. [2, 18]. This is in the case of hydrodynamic lubrication and even without any lubricant; the independence of the friction force of the contact area is explained by rather widely accepted ideas with the plastic flow of the materials at the surface region, etc. [1,2]. In the last decades, the interest has increased, and several theories basing different mechanisms were published and experimentally examined that explain friction and wear at different circumstances and the results are not like to each other nor to Coulomb’s law [2]. Finally, here an accurately accountable model has been given that may be assumed friction if we pretend not knowing its origin and the law differs significantly from the nearly exclusively used Coulomb’s law. This example supports the idea that friction can be described but with a simple and uniform theory. Assume that the roughness of the surfaces involves perpendicular motion and visco-elastic waves are generated. It is similar when a car goes on a rough road. The part of the driving force due to the energy loss in the shock absorber (visco- elastic loss in the bulks of the bodies) does not depend on the normal force but on the masses of the bodies and on the velocity. The function is rather complicated and at high velocities it is proportional to the velocity and independent of the masses or the normal force.

Appendix

Lemma 1

Assume a set of some non-liear Onsager equations

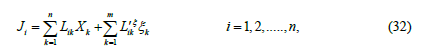
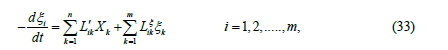
Without violating the generality, we may suppose that the coeffcients Lξ_ik do not depend on any X_k . If they do, introduce the auxiliary quantities

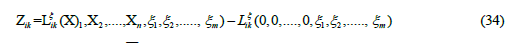
Because any Z_ik is zero if all the X’s are zero, they can be cast into the form

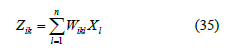
where all W _ikl are continuous. With them, the evolution equations 33 of the dynamic variables, after some rearrangements, turn to

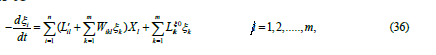
where the coefficients 0 ik Lξ are independent of the X’s. The same procedure leads to the statement, that the coefficients ik L′ξ are also independent of the X’s.

Lemma 2

The ratio of any two 0 ik Lξ coefficients of eq. (36) is independent of the thermodynamic forces. Assume the set of the differential equations

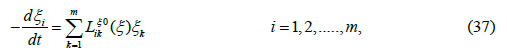
which gives account on the evolution of the dynamic variables toward the equilibrium. The differential equation of the trajectories is obtained in the form

c

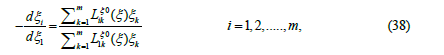
The trajectories are well defined and a manifold of curves, referred here as “linear trajectory”, can be defined by the equations

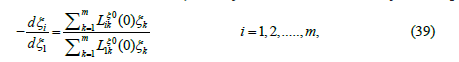
Now map any trajectory to the linear trajectory to which it fits best at equilibrium. The mapping is a bijection, Next map the points of the space of the dynamic variable to the one the entropy of which is the same and lies on the corresponding linear trajectory. The mapping in two dimensions is shown in Figure (7). This way we obtain a new representation of the dynamic variables the trajectories of which is defined by the equations of the linear trajectories, eq. (39). With the help of the latest result and combining the above equations for the trajectories, eqs. (38) and (39), moreover, introducing the function

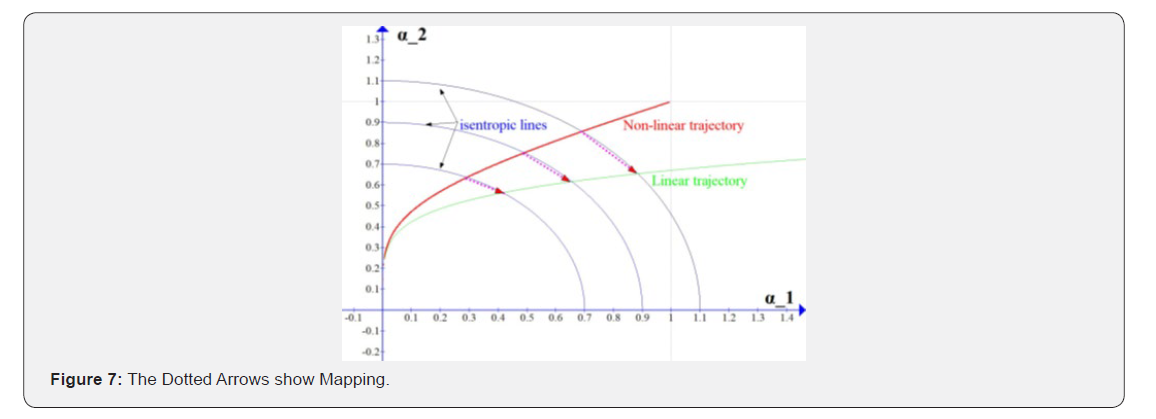
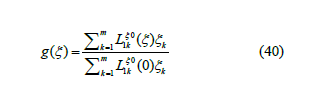
the equations for the relaxation, eq. (37), can be reformulated to

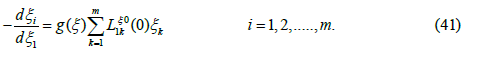
This means that the Onsager coefficients in the non-linear theory are the same as in the linear theory multiplied with the same function of the dynamic variables.

To know more articles in Insights in Mining Science & Technology please click on

https://juniperpublishers.com/imst/index.php

 To know more about Juniper Publishers please click on

https://juniperpublishers.com/index.php