Juniper Publishers - An Analytical Model for Axial Force Transfer and the Maximum Compression Point of Work Strings in Extend Reach Drilling
Insights
in Mining Science & Technology
Abstract
Complex work string dynamics are often observed when one is investigating the limit of Extended Reach Drilling (ERD), yet the underlying physical causes of anomalous problems are often not fully understood and is thus a topic of ongoing research interest. Theoretical models capturing tubular dynamics have been previously proposed to analyze force transfer in work strings, yet there is significant confusion regarding these models because their published versions are not entirely consistent and, in many cases, do not meet engineering requirement. Further confusion is introduced through variations in pin-pointing locations where axial compression in the work strings should be checked for mechanical integrity. A simple and yet rigorous mathematical model is essential for adequate prediction of axial compression profiles in work strings for ERD. This article presents a simplified tubular mechanics model for describing axial force transfer under ERD conditions. We discuss the model in finding the point of peak compression in casing strings. This point is predicted to be in the arc section near the heel of a horizontal wellbore, under borehole drilling, and casing running conditions. The exact location of the peak axial compression changes with pipe-wall friction coefficient. For the friction coefficient in the range of 0.15 to 0.35, this point occurs in the range of inclination angle between 70.7o and 81.5o, averaging 76.1o. The model can also be used for other purposes, including prediction of depth limit, bottom hole assembly (BHA) design, and locking up analysis of coiled tubing (CT) strings.
Keywords: Extended-reach-wells; Casing design, Work strings; Drilling; Stability
Introduction
Extended reach wells (ERW) are horizontal wells used for reaching oil and gas resources located laterally and far from well location. ERW has become a common practice over the last two decades for improving field economics. Extended Reach Drilling (ERD) is a technique to drill directional/horizontal wells beyond the routine capabilities of drilling rigs and tools. ERD was initiated in 1980’s and rapidly evolved during the 1990’s [1-4]. Naegel et al. [5] reported an ERD well with a 20,341.2 ft horizontal departure at 5,577 ft true vertical depth (TVD). ERD continued in the past two decades with new record updated every a few years [6-11]. Armstrong and Evans [12] reported planning and execution of an offshore ERD well of a total measured depth (MD) of 37,165 ft with TVD of 6,938 ft, and horizontal displacement (HD) of 33,682 ft. Tskhadaya et al. [13] presented a design of ERD for an Arctic well depth of 49,212.6 ft and horizontal borehole depth of 4,921.3 ft.
Special technical issues in ERD include rig requirement, borehole stability, cuttings transport, data acquisition, and drill string design. In the particular topic of our ongoing research interest, i.e., tubular mechanics of work strings (drill string, coiled tubing string, and casing string), Nixon et al. [14] presented techniques to solve the problems associated with excessive torque during ERD. Hill et al. [15] discussed designing and qualifying drill strings for ERD while Mason and Judzis [16] discussed the limit of ERD, and Suggett and Smith [17] addressed the issue of ERD limit for rig capacity. Bell et al. [18] reported an application of significant increases in the lateral reach of a number of ERW’s. Samuel [19] presented a new well-path design that can extend the reach of ERW through reducing torque and drag using curvature and torsion discontinuities. Agbaji [20] presented an algorithm that would set forth design for drilling programs suitable to ERD. Vestavik et al. [21] presented a potential application of Reelwell Drilling Method (RDM) to widen the envelope of ERD through reductions of torque and drag and Equivalent Circulating Density (ECD) gradient, and optimization of hydraulic weight on bit. Newman et al. [22] explained that for ERD with coiled tubing (CT) where a limitation on the horizontal displacement occurs due to frictional forces, the friction can cause helical buckling and lead to lockup of the CT strings, thus limiting reach. Gupta et al. [23] discussed several key challenges in ERD, including high torque and drag due to high friction forces.
Theoretical models capturing tubular dynamics have been previously proposed to analyze force transfer in the work strings used in ERD, yet there is significant confusion regarding these models because they are are not entirely consistent and, are hard to use due to model complexity. Also, no model has been found to have the capacity of pin-pointing the locations where the axial compression in work strings should be checked for mechanical integrity. A simple and rigorous analytical solution in closed form is presented in this work for adequate prediction of axial compression profiles in the work strings for ERD. We discuss the model in finding the point of peak compression in casing strings. This point is predicted to occur in the arc section, near the heel of a horizontal wellbore, under borehole drilling and casing running conditions. The model can also be used for other purposes, including prediction of depth limit, BHA design, and lockup condition analysis of CT strings.
Mathematical Model
Figure 1 illustrates a simplified configuration of a work string (drill string, casing string, or coiled tubing string) used in horizontal well construction engineering. Two-dimensional well trajectory of build-and-hold type is considered. The string is assumed to contact the lower side of borehole due to gravity in the curve and slant/horizontal sections without buckling. Owing to its large length-to-diameter ratio, the string is considered to be ropelike without stiffness. It is subjected to axial tension/compression but not bending moment.
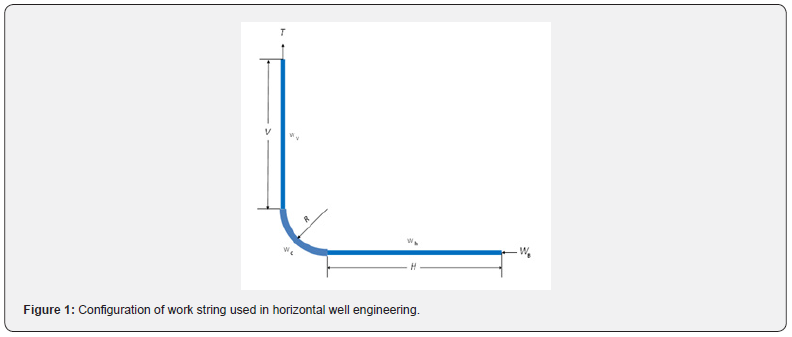
The axial compression force in the vertical section of string increases with depth due to gravity. Its value at the kick-of-point (KOP) is expressed as

Where F0 is the axial compressive force in the string at KOP, wv is the weight per length of the string in the vertical section, V is the length of vertical string section, and T is the tension at the surface (hook load). In the down-ward motion, the axial compression force in the horizontal section increases with the distance from the end of string (toe of horizontal well) due to friction. The axial compression force at the heel reaches to
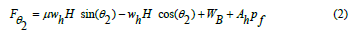
Where 2fθ is the axial compressive force in the string at the heel of horizontal well, μ is the friction coefficient between the string and borehole wall, wh is the weight per length of the string in the slant/horizontal section, H is the length of string in the slant/horizontal section, θ2 is the inclination angle at the heel point, WB is the force acting back by the borehole bottom (weight on bit in drilling condition), Ah is the cross-sectional area of string in the horizontal section, and pf is the fluid pressure in the bottom hole. If the slant section is truly horizontal (θ2 = π/2), Eq. (2) degenerates to

where Fπ /2 is the axial compressive force at the heel.
Because the axial compression force in the string is a continuous function of length, its value is expected to reach a maximum between F0 and Fπ /2 in the curved section. The axial compression force in the curve section is expressed as (see Appendix A for derivation):
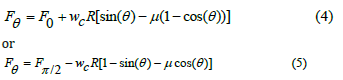
Where wc is the weight per length in the curved section, and R is the radius of curvature.
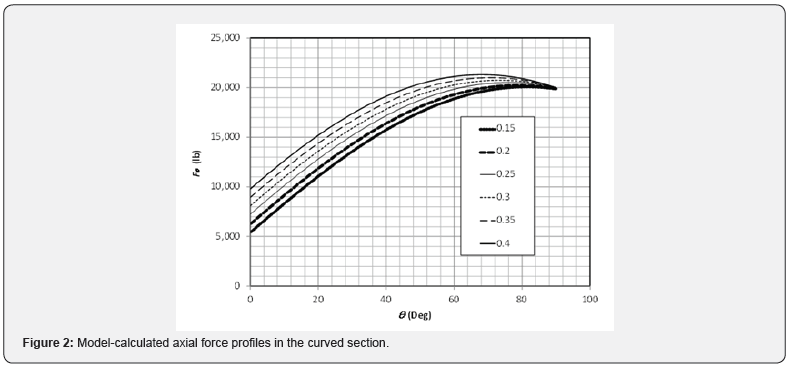
Equation (5) is plotted in Figure 2 for Fπ/2 = 20,000 lb, wc = 17 lb/ft, and R = 1,000 ft for friction coefficient values ranging from 0.15 to 0.40. It indicates that a maximum value of axial compression exists near the heel, depending on friction coefficient.
The maximum axial compression force occurs at a point where the function is stationary. The derivative of this function is

Model Applications
This mathematical model can be used in casing design, drill string design, and coiled tubing stability analysis in horizontal well engineering. Two examples are illustrated in this section.
Casing Design. Casing strings for horizontal wells are designed considering multiple stress components that cause:
a) Burst failure due to net bust pressure
b) Collapse failure due to net collapse pressure
c) Tensile/compressive failure due to axial forces (gravity, friction, and bending)
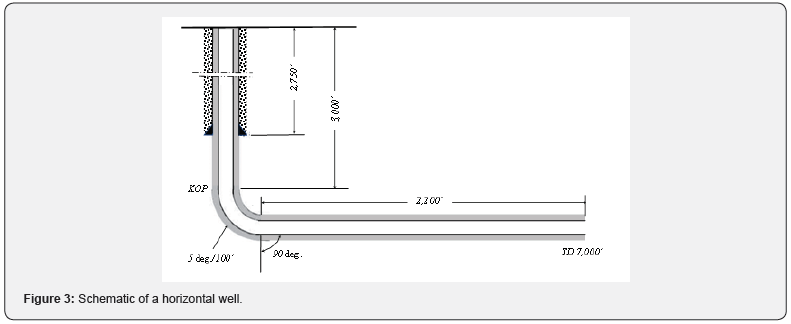
The axial compression force can reduce the casing’s burst resistance performance. Suppose a 5½” J-55, 17 lb/ft, production casing is selected to run in the curve section of the borehole shown in Figure 3. The mud weight is 12.5ppg and friction coefficient is 0.30. It is required to check the reduced burst pressure resistance of the casing due to axial compression.
The API burst pressure resistance of the casing is [24]:
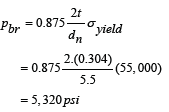
Where t is the thickness, dn is the nominal pipe diameter, and σyield is the yield stress
Radius of curvature is [24]:
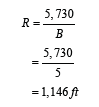
Axial compression at heel is
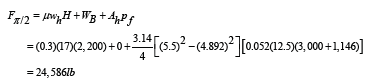
A complete profile of axial force was calculated with the mathematical model and is shown in Figure 4. It shows a maximum axial compression near, but not at the heel.
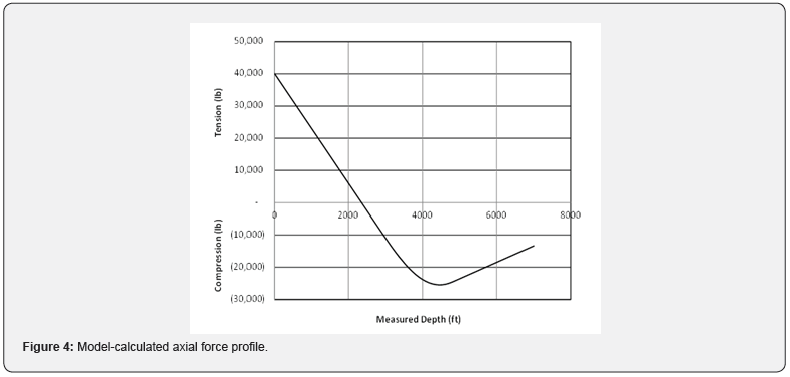
The maximum axial compression is
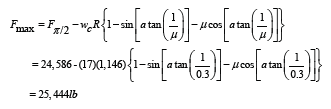
The maximum axial stress due to weight and friction is

Bending stress is
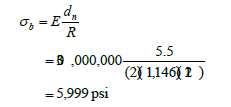
Where σb is the bending stress, and E is the Young’s modulus of elasticity. The total axial compression is
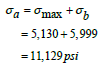
API tangential stress factor for burst is [24]:
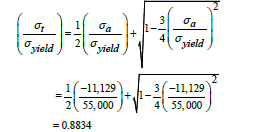
Where σt is the tangential stress.
Reduced burst pressure resistance of the casing is [24]:
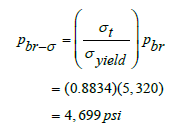
which means that the axial compression will reduce burst pressure resistance of the casing from 5,320 psi to 4,699 psi, or by 12%.
Drill String Design. Drill strings for horizontal wells consists of drill collar design, considering friction forces in the curved and horizontal sections, under drilling conditions (down-ward motion), and drill pipe design considering over-pull under, tripping-out conditions (upward motion).
Consider the situation shown in Figure 5. Design parameters are given in Table 1. Equation (2) gives
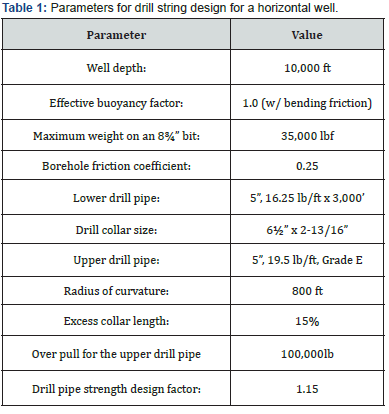
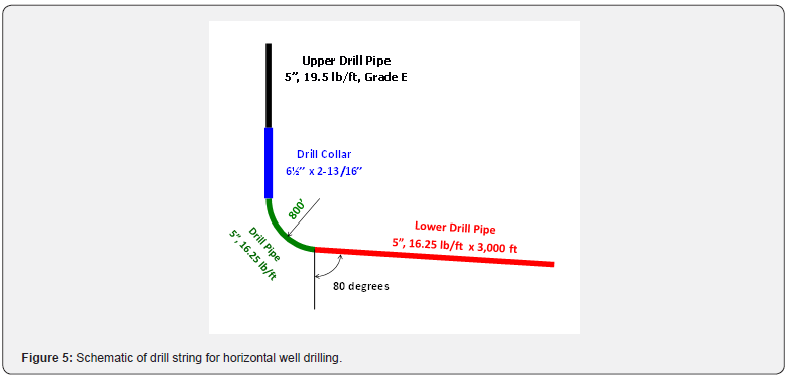
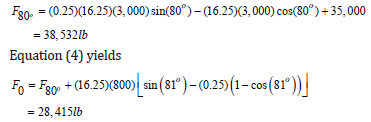
The required drill collar weight is (1.15)(28,415) or 32,677 lb. Based on the unit weight of 92 lb/ft of the drill collar, the required drill collar length is (32,677)/(92) or 356 ft.
For drill pipe design, the curved linear length of the arc section is (800)(80)/(57.3) or 1,117 ft. The weight of the lower drill pipe is (16.25)(3,000+1,117) or 66,900 lb. Based on the tensile capacity of Grade G steel pipe, 436,000 lb, the maximum pull on the Grade G drill pipe with design factor is (436,000)/(1.15) or 379,130 lb. The maximum permissible weight of Grade G pipe string with over pull of 100,000 lb is
379,130 – 66,900 – 32,677 – 100,000 = 179,553 lb The maximum permissible length of this pipe string is (179,553)/(19.5) or 9,208 ft, which is greater than the needed length of 10,000 – 3,000 – 1,117 – 356 = 5,527 ft,
Conclusion
An analytical model for axial force transfer and the maximum compression point in work strings for ERD was developed in this investigation. The following conclusions are drawn.
a) The maximum axial compression point is in the arc section near the heel of a horizontal well when the work string is in down-ward motion. The exact location of the maximum axial compression changes with casing-wall friction coefficient. For μ = 0.15 ~ 0.35 in horizontal well engineering, the maximum axial compression occurs with θ = 70.7o ~ 81.5o, averaging 76.1o.
b) When applied to casing design, the maximum compression point model can be easily used to evaluate the reduction of the casing’s burst resistance performance. Results show that the casing’s burst resistance performance can be significantly reduced due to axial compression (12% in the illustrative example).
c) When applied to drill string design, the axial force transfer model can be easily utilized to determine the required drill collar weight and length, which is further used for selecting drill pipe string.
d) Future studies should validate the mathematical model and investigate the applicability of the model to CT stability analysis and predict the depth limit of ERD.
To Know More
About Insights in Mining Science & Technology Please click on:
https://juniperpublishers.com/imst/index.php
For more Open Access
Journals in Juniper Publishers please click on:
https://juniperpublishers.com/index.php
For more about Juniper Publishers Please click on:
https://www.zoominfo.com/c/juniper-publishers-inc/370428819


Comments
Post a Comment